算法学习之旅，终点亦是起点

最近在学习算法，做过的题会提交在这里 我的 LeetCode ，欢迎围观。

数据结构

脑图：https://naotu.baidu.com/file/0a53d3a5343bd86375f348b2831d3610?token=5ab1de1c90d5f3ec

• 一维：

  基础：数组 array (string), 链表 linked list

  高级：栈 stack, 队列 queue, 双端队列 deque, 集合 set, 映射 map (hash or map), etc

• 二维：

  基础：树 tree, 图 graph

  高级：二叉搜索树 binary search tree (red-black tree, AVL), 堆 heap, 并查集 disjoint set, 字典树 Trie, etc

• 特殊：

  位运算 Bitwise, 布隆过滤器 BloomFilter

  LRU Cache

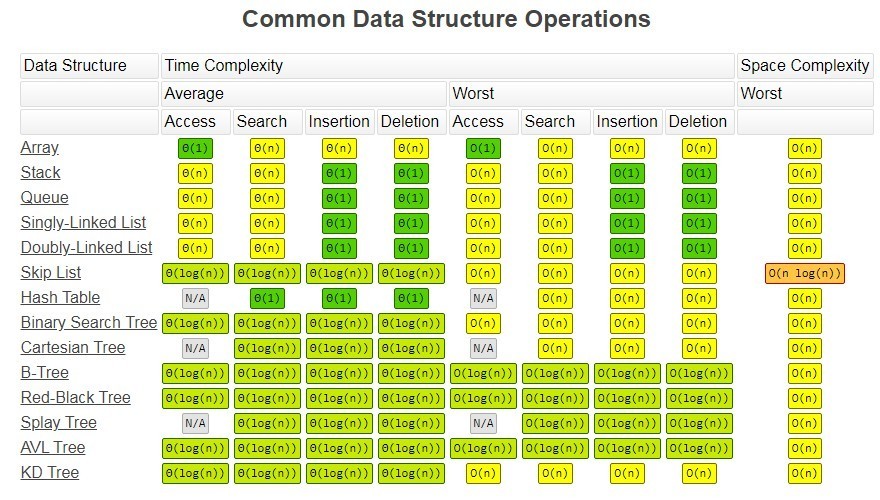
时间复杂度

https://www.bigocheatsheet.com/

算法

• If-else, switch —> branch

• for, while loop —> Iteration

• 递归 Recursion (Divide & Conquer, Backtrace)

• 搜索 Search: 深度优先搜索 Depth first search, 广度优先搜索 Breadth first search, A*, etc

• 动态规划 Dynamic Programming

• 二分查找 Binary Search

• 贪心 Greedy

• 数学 Math , 几何 Geometry

刷题路线分享

基础

• 两数之和（简单）
• 有效的括号（简单）
• 字符串解码（中等）
• LRU 缓存机制（困难）
• 实现 Trie（前缀树）（中等）
• 添加与搜索单词 - 数据结构设计（中等）
• 单词搜索 II （困难）
• 找不同（简单）
• 单词规律（简单）
• 字符串中的第一个唯一字符（简单）
• 无重复字符的最长子串（中等）
• 最小覆盖子串（困难）
• 合并两个有序链表（简单）
• 环形链表（简单）
• 环形链表 II （中等）
• 反转链表（简单）
• 反转链表 II （中等）
• 旋转链表（中等）
• 排序链表
• 链表中倒数第 k 个节点
• 两两交换链表中的节点（中等）
• 按奇偶排序数组（简单）
• 按奇偶排序数组 II （简单）
• 有序数组的平方（简单）
• 山脉数组的峰顶索引（简单）
• 搜索旋转排序数组（困难）
• 搜索旋转排序数组 II （中等）
• 寻找旋转排序数组中的最小值（中等）
• 寻找旋转排序数组中的最小值 II （困难）
• 搜索二维矩阵（中等）
• 等式方程的可满足性（中等）
• 朋友圈（中等）
• 账户合并（中等）

深度优先搜索

• 二叉树的最大深度（简单）
• 路径总和（简单）
• 路径总和 II （中等）
• 被围绕的区域（中等）
• 岛屿数量（中等）
• 岛屿的最大面积（中等）
• 在二叉树中分配硬币（中等）

回溯

• 括号生成（中等）
• N 皇后（困难）
• N 皇后 II （困难）
• 解数独 （中等）
• 不同路径 III （困难）
• 单词搜索（中等）

分治

• 搜索二维矩阵 II （中等）
• 合并 K 个排序链表（中等）
• 为运算表达式设计优先级（中等）
• 给表达式添加运算符（困难）
• 数组中的第 K 个最大元素（中等）
• 最接近原点的 K 个点（中等）
• 鸡蛋掉落（困难）

动态规划

• 使用最小花费爬楼梯（简单）
• 爬楼梯（简单）
• 不同路径（简单）
• 最小路径和 （中等）
• 最大子序和 （简单）
• 乘积最大子数组（中等）
• 买卖股票的最佳时机（简单）
• 买卖股票的最佳时机 II （简单）
• 买卖股票的最佳时机 III （困难）
• 买卖股票的最佳时机 IV （困难）
• 最佳买卖股票时机含冷冻期（中等）
• 买卖股票的最佳时机含手续费（中等）
• 零钱兑换 （中等）
• 零钱兑换 II （中等）
• 编辑距离（困难）
• 不同的子序列（困难）
• 柱状图中最大的矩形（困难）
• 最大矩形（困难）
• 最大正方形（中等）
• 最低票价（中等）
• 区域和检索 - 数组不可变（简单）
• 二维区域和检索 - 矩阵不可变（中等）
• 最长上升子序列 （中等）
• 鸡蛋掉落（困难）

部分代码模板 （仅供参考）

并不是题目答案，只是说明大部分题目有套路可循；主要是java、python的版本，或者伪代码，应该能看懂。

递归

// java
public  void  recur(int level, int param) {

	// terminator

	if (level > MAX_LEVEL) {

		// process result

		return;

	}

	// process current logic

	process(level, param);

	// drill down

	recur( level: level + 1, newParam);

	// restore current status

}

分治、回溯

// java
private  static  int  divide_conquer(Problem problem, ) {

	if (problem == NULL) {

		int  res = process_last_result();

		return res;

	}

	subProblems = split_problem(problem)

	res0 = divide_conquer(subProblems[0])

	res1 = divide_conquer(subProblems[1])

	result = process_result(res0, res1);

	return result;

}

DFS

递归写法

// java
public  List<List<Integer>> levelOrder(TreeNode root) {

	List<List<Integer>> allResults = new  ArrayList<>();

	if(root==null){

		return allResults;

	}

	travel(root,0,allResults);

	return allResults;

}

private  void  travel(TreeNode root,int level,List<List<Integer>> results){

	if(results.size()==level){

		results.add(new  ArrayList<>());

	}

	results.get(level).add(root.val);

	if(root.left!=null){

		travel(root.left,level+1,results);

	}

	if(root.right!=null){

		travel(root.right,level+1,results);

	}

}

非递归写法

# Python
def  DFS(self, tree):

	if tree.root is  None:

		return []

	visited, stack = [], [tree.root]

	while stack:

		node = stack.pop()

		visited.add(node)

		process (node)

		nodes = generate_related_nodes(node)

		stack.push(nodes)

	# other processing work

	...

BFS

# Python
def  BFS(graph, start, end):

	visited = set()

	queue = []

	queue.append([start])

	while queue:

		node = queue.pop()

		visited.add(node)

		process(node)

		nodes = generate_related_nodes(node)

		queue.push(nodes)

	# other processing work

	...

贪心算法

贪心算法是在当前情况下做出的最优决定，它只考虑眼前，获得的是局部的最优解，并且，希望通过每次获得局部最优解最后找到全局的最优解。

二分查找

// Java
public  int  binarySearch(int[] array, int target) {

	int  left = 0, right = array.length - 1, mid;

	while (left <= right) {

		mid = (right - left) / 2 + left;

		if (array[mid] == target) {

			return mid;

		} else  if (array[mid] > target) {

			right = mid - 1;

		} else {

			left = mid + 1;

		}

	}

	return -1;

}

动态规划

• 动态规划 和 递归或者分治 没有根本上的区别（关键看有无最优的子结构）

• 共性：找到重复子问题

• 差异性：最优子结构、中途可以淘汰次优解

DP顺推模板

# 伪代码
function DP():

	dp = [][] # 二维情况

	for i = 0 .. M {

		for j = 0 .. N {

			dp[i][j] = _Function(dp[i’][j’]...)

		}

	}

	return dp[M][N];

Trie 树（字典树）

// java
class  Trie {

	private  boolean  isEnd;

	private  Trie[] next;

	/** Initialize your data structure here. */

	public  Trie() {

		isEnd = false;

		next = new  Trie[26];

	}

	/** Inserts a word into the trie. */

	public  void  insert(String  word) {

		if (word == null || word.length() == 0) return;

		Trie  curr = this;

		char[] words = word.toCharArray();

		for (int  i = 0;i < words.length;i++) {

			int  n = words[i] - 'a';

			if (curr.next[n] == null) curr.next[n] = new  Trie();

			curr = curr.next[n];

		}

		curr.isEnd = true;

	}

	/** Returns if the word is in the trie. */

	public  boolean  search(String  word) {

		Trie  node = searchPrefix(word);

		return node != null && node.isEnd;

	}

	/** Returns if there is any word in the trie that starts with the given prefix. */

	public  boolean  startsWith(String  prefix) {

		Trie  node = searchPrefix(prefix);

		return node != null;

	}

	private  Trie  searchPrefix(String  word) {

		Trie  node = this;

		char[] words = word.toCharArray();

		for (int  i = 0;i < words.length;i++) {

			node = node.next[words[i] - 'a'];

			if (node == null) return  null;

		}

		return node;

	}

}

并查集

// java
class  UnionFind {

	private  int  count = 0;

	private  int[] parent;

	public  UnionFind(int  n) {

		count = n;

		parent = new  int[n];

		for (int  i = 0; i < n; i++) {

			parent[i] = i;

		}

	}

	public  int  find(int  p) {

		while (p != parent[p]) {

			parent[p] = parent[parent[p]];

			p = parent[p];

		}

		return p;

	}

	public  void  union(int  p, int  q) {

		int  rootP = find(p);

		int  rootQ = find(q);

		if (rootP == rootQ) return;

		parent[rootP] = rootQ;

		count--;

	}

}

布隆过滤器

// java
public  class  BloomFilter {

	private  static  final  int  DEFAULT_SIZE = 2 << 24;

	private  static  final  int[] seeds = new  int[] { 5, 7, 11, 13, 31, 37, 61 };

	private  BitSet  bits = new  BitSet(DEFAULT_SIZE);

	private  SimpleHash[] func = new  SimpleHash[seeds.length];

	public  BloomFilter() {

		for (int  i = 0; i < seeds.length; i++) {

			func[i] = new  SimpleHash(DEFAULT_SIZE, seeds[i]);

		}

	}

	public  void  add(String  value) {

		for (SimpleHash  f  : func) {

			bits.set(f.hash(value), true);

		}

	}

	public  boolean  contains(String  value) {

		if (value == null) {

			return  false;

		}

		boolean  ret = true;

		for (SimpleHash  f  : func) {

			ret = ret && bits.get(f.hash(value));

		}

		return ret;

	}

	// 内部类，simpleHash

	public  static  class  SimpleHash {

		private  int  cap;

		private  int  seed;

		public  SimpleHash(int  cap, int  seed) {

			this.cap = cap;

			this.seed = seed;

		}

		public  int  hash(String  value) {

			int  result = 0;

			int  len = value.length();

			for (int  i = 0; i < len; i++) {

				result = seed * result + value.charAt(i);

			}

			return (cap - 1) & result;

		}

	}

}

LRU Cache

// java 哈希表 + 双链表
class  LRUCache {

	/**

	* 缓存映射表

	*/

	private  Map<Integer, DLinkNode> cache = new  HashMap<>();

	/**

	* 缓存大小

	*/

	private  int  size;

	/**

	* 缓存容量

	*/

	private  int  capacity;

	/**

	* 链表头部和尾部

	*/

	private  DLinkNode  head, tail;

	public  LRUCache(int  capacity) {

		//初始化缓存大小，容量和头尾节点

		this.size = 0;

		this.capacity = capacity;

		head = new  DLinkNode();

		tail = new  DLinkNode();

		head.next = tail;

		tail.prev = head;

	}

	/**

	* 获取节点

	* @param  key 节点的键

	* @return 返回节点的值

	*/

	public  int  get(int  key) {

		DLinkNode  node = cache.get(key);

		if (node == null) {

			return -1;

		}

		//移动到链表头部

		(node);

		return  node.value;

	}

	/**

	* 添加节点

	* @param  key 节点的键

	* @param  value 节点的值

	*/

	public  void  put(int  key, int  value) {

		DLinkNode  node = cache.get(key);

		if (node == null) {

			DLinkNode  newNode = new  DLinkNode(key, value);

			cache.put(key, newNode);

			//添加到链表头部

			addToHead(newNode);

			++size;

			//如果缓存已满，需要清理尾部节点

			if (size > capacity) {

				DLinkNode  tail = removeTail();

				cache.remove(tail.key);

				--size;

			}

		} else {

			node.value = value;

			//移动到链表头部

			moveToHead(node);

		}

	}

	/**

	* 删除尾结点

	*

	* @return 返回删除的节点

	*/

	private  DLinkNode  removeTail() {

		DLinkNode  node = tail.prev;

		removeNode(node);

		return node;

	}

	/**

	* 删除节点

	* @param  node 需要删除的节点

	*/

	private  void  removeNode(DLinkNode  node) {

		node.next.prev = node.prev;

		node.prev.next = node.next;

	}

	/**

	* 把节点添加到链表头部

	*

	* @param  node 要添加的节点

	*/

	private  void  addToHead(DLinkNode  node) {

		node.prev = head;

		node.next = head.next;

		head.next.prev = node;

		head.next = node;

	}

	/**

	* 把节点移动到头部

	* @param  node 需要移动的节点

	*/

	private  void  moveToHead(DLinkNode  node) {

		removeNode(node);

		addToHead(node);

	}

	/**

	* 链表节点类

	*/

	private  static  class  DLinkNode {

		Integer  key;

		Integer  value;

		DLinkNode  prev;

		DLinkNode  next;

		DLinkNode() {

		}

		DLinkNode(Integer  key, Integer  value) {

			this.key = key;

			this.value = value;

		}

	}

}

十大经典排序算法

阅读：https://www.cnblogs.com/onepixel/p/7674659.html

图片来源于上文

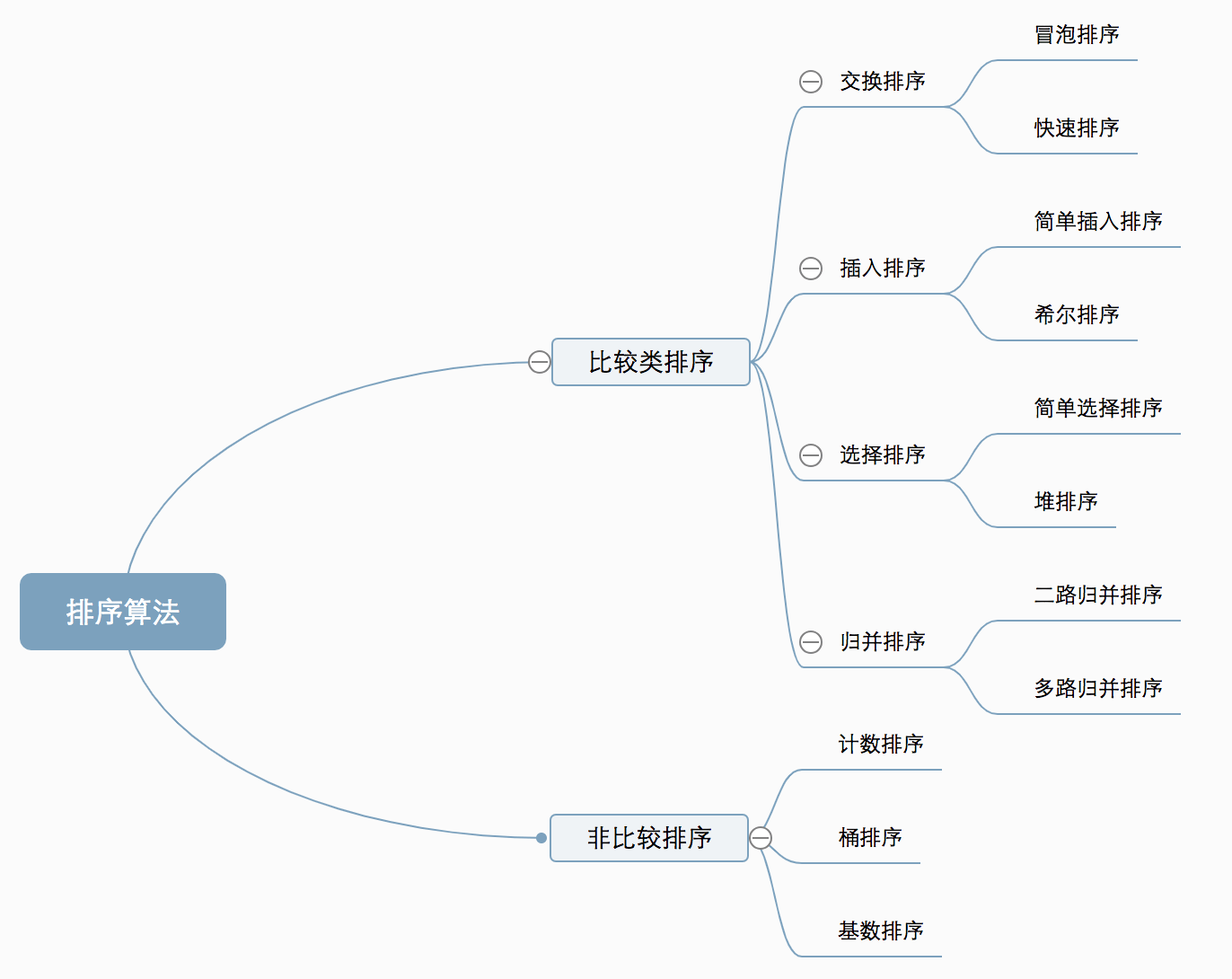
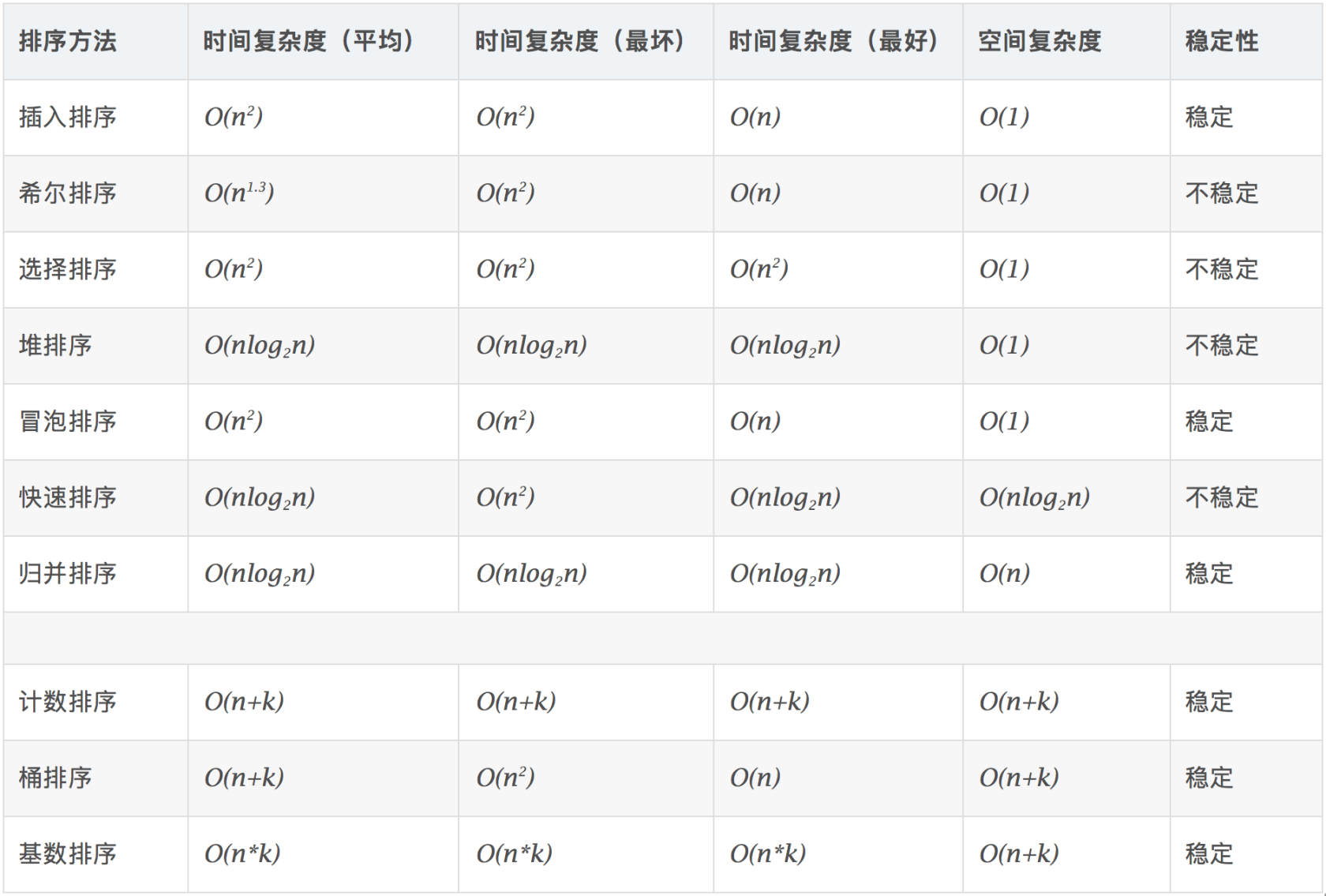
快速排序

// java
public  static  void  quickSort(int[] array, int begin, int end) {

	if (end <= begin) return;

	int  pivot = partition(array, begin, end);

	quickSort(array, begin, pivot - 1);

	quickSort(array, pivot + 1, end);

}

static  int  partition(int[] a, int begin, int end) {

	// pivot: 标杆位置，counter: 小于pivot的元素的个数

	int  pivot = end, counter = begin;

	for (int  i = begin; i < end; i++) {

		if (a[i] < a[pivot]) {

			int  temp = a[counter]; a[counter] = a[i]; a[i] = temp;

			counter++;

		}

	}

	int  temp = a[pivot]; a[pivot] = a[counter]; a[counter] = temp;

	return counter;

}

归并排序

// java
public  static  void  mergeSort(int[] array, int left, int right) {

	if (right <= left) return;

	int  mid = (left + right) >> 1; // (left + right) / 2

	mergeSort(array, left, mid);

	mergeSort(array, mid + 1, right);

	merge(array, left, mid, right);

}

public  static  void  merge(int[] arr, int left, int mid, int right) {

	int[] temp = new  int[right - left + 1]; // 中间数组

	int  i = left, j = mid + 1, k = 0;

	while (i <= mid && j <= right) {

		temp[k++] = arr[i] <= arr[j] ? arr[i++] : arr[j++];

	}

	while (i <= mid) temp[k++] = arr[i++];

	while (j <= right) temp[k++] = arr[j++];

	for (int  p = 0; p < temp.length; p++) {

		arr[left + p] = temp[p];

	}

	// 也可以用 System.arraycopy(a, start1, b, start2, length)

}

堆排序

// java
public  static  void  heapSort(int[] array) {

	if (array.length == 0) return;

	int  length = array.length;

	for (int  i = length / 2-1; i >= 0; i-)

		heapify(array, length, i);

	for (int  i = length - 1; i >= 0; i--) {

		int  temp = array[0]; array[0] = array[i]; array[i] = temp;

		heapify(array, i, 0);

	}

}

static  void  heapify(int[] array, int length, int i) {

	int  left = 2 * i + 1, right = 2 * i + 2；

	int  largest = i;

	if (left < length && array[left] > array[largest]) {

		largest = left;

	}

	if (right < length && array[right] > array[largest]) {

		largest = right;

	}

	if (largest != i) {

		int  temp = array[i]; array[i] = array[largest]; array[largest] = temp;

		heapify(array, length, largest);

	}

}

结语

光说不练假把式，重要的是动手做题。